1. 基数估计算法
Linear counting
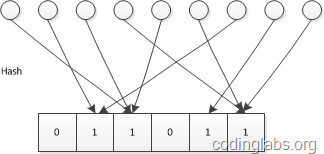
该算法用于估测数据基数,也就是说有多少不同元素,采用方法非常简单,将数据哈希到长度为m的数组,访问到的位置就置为1
设有一哈希函数$H$,其哈希结果空间有m个值(最小值0,最大值m-1),且哈希结果均匀分布。
使用一个长度为$m$的bitmap,每个bit为一个bucket(初始化为0)。
设一个集合的基数为$n$,此集合所有元素通过$H$哈希到bitmap中,如果某一个元素被哈希到第k个比特并且第k个比特为0,则将其置为1。
- 当集合所有元素哈希完成后,设bitmap中还有$u$个bit为0。
我们可以近似认为$n$足够大的时候,哈希的结果服从均匀分布,
那么最后设集合基数为n的最大似然估计为:
LC需要的空间只有传统bitmap的$\frac{1}{10}$, 从渐进的角度看空间复杂度仍为$O(N_{max})$
详细推导过程见:https://blog.csdn.net/wbin233/article/details/78752597
论文:- Whang, Kyu-Young, Brad T. Vander-Zanden, and Howard M. Taylor. “A linear-time probabilistic counting algorithm for database applications.” ACM Transactions on Database Systems (TODS) 15.2 (1990): 208-229.
FM Sketch(PCSA)
该算法是基于概率来估计基数,首先我们根据数据随机情况观察二进制的性质,可以发现末尾有k个连续0的情况出现次数是按比例缩小的,因此我们基于这个观察得出估计方法
首先我们随机一个哈希函数将数据映射到一个二进制长度为L的空间内(即 $[0,2^L-1]$),我们记录BITMAP来标记是否出现一个数后尾恰好有连续i个0,这样显然根据访问的概率就可以估计数据基数,我们取在bitmap中第一个为0的位置,即我们没有映射后末尾恰好有$k$个0的key,因此我们用$k$来近似$logn$,显然这样数据是偏小的,论文根据计算添加了偏差参数$E(k)=log\phi n, \phi = 0.77351…$
显然这样还是不太准确,于是就采用了多次哈希的方式,我们利用得到的$k$的均值来进行估计
论文:Flajolet, Philippe, and G. Nigel Martin. “Probabilistic counting algorithms for data base applications.” Journal of computer and system sciences 31.2 (1985): 182-209.
LogLog
顾名思义,就是利用$loglogn$的空间来实现估测基数的算法。可以说基本就是FM的优化,我们记录$p(x)$表示对于想哈希之后末尾有$p(x)$个0,那么其实我们只需要记录$max(p(x))$即可,因此该空间为$loglogn$的
那么同样,我们可以采用将数据随机分桶统计,通过求max的平均值来估测
HyperLogLog算法使用调和平均值将它们组合成原始基数的估计值
参考:https://zhuanlan.zhihu.com/p/271186546
hyperloglog demo:http://content.research.neustar.biz/blog/hll.html)
基数估计算法(包括HLL、AC)