伯努利实验
在认识为什么HyperLogLog能够使用极少的内存来统计巨量的数据之前,要先认识下伯努利试验。
硬币拥有正反两面,一次的上抛至落下,最终出现正反面的概率都是50%。假设一直抛硬币,直到它出现正面为止,我们记录为一次完整的试验,间中可能抛了一次就出现了正面,也可能抛了4次才出现正面。无论抛了多少次,只要出现了正面,就记录为一次试验。这个试验就是伯努利试验。
那么对于多次的伯努利试验,假设这个多次为n次。就意味着出现了n次的正面。假设每次伯努利试验所经历了的抛掷次数为k。第一次伯努利试验,次数设为k1,以此类推,第n次对应的是kn
其中,对于这n次伯努利试验中,必然会有一个最大的抛掷次数k,例如抛了12次才出现正面,那么称这个为k_max,代表抛了最多的次数。
伯努利试验容易得出有以下结论:
- n 次伯努利过程的投掷次数都不大于 k_max。
- n 次伯努利过程,至少有一次投掷次数等于 k_max
最终结合极大似然估算的方法,发现在n和k_max中存在估算关联:n = 2^(k_max) 。这种通过局部信息预估整体数据流特性的方法似乎有些超出我们的基本认知,需要用概率和统计的方法才能推导和验证这种关联关系。
例如下面的样子:
1 | 第一次试验: 抛了3次才出现正面,此时 k=3,n=1 |
假设上面例子中实验组数共3组,那么 k_max = 6,最终 n=3,我们放进估算公式中去,明显: 3 ≠ 2^6 。也即是说,当试验次数很小的时候,这种估算方法的误差是很大的。
估算优化
在上面的3组例子中,我们称为一轮的估算。如果只是进行一轮的话,当 n 足够大的时候,估算的误差率会相对减少,但仍然不够小。
那么是否可以进行多轮呢?例如进行 100 轮或者更多轮次的试验,然后再取每轮的 k_max,再取平均数,即: k_mx/100。最终再估算出 n。下面是LogLog的估算公式:
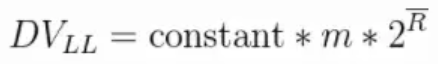
上面公式的
DVLL对应的就是n,constant是修正因子,它的具体值是不定的,可以根据实际情况而分支设置。m代表的是试验的轮数头上有一横的
R就是平均数:(k_max_1 + ... + k_max_m)/m
这种通过增加试验轮次,再取k_max平均数的算法优化就是LogLog的做法。
而 HyperLogLog和LogLog的区别就是,它采用的不是平均数,而是调和平均数。调和平均数比平均数的好处就是不容易受到大的数值的影响。下面举个例子:
求平均工资: A的是1000/月,B的30000/月。采用平均数的方式就是: (1000 + 30000) / 2 = 15500, 采用调和平均数的方式就是: 2/(1/1000 + 1/30000) ≈ 1935.484, 明显地,调和平均数比平均数的效果是要更好的。下面是调和平均数的计算方式,∑ 是累加符号
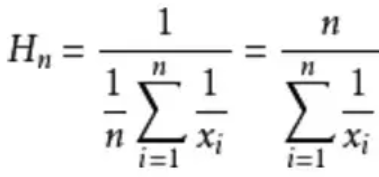
扯上关系
上面的内容我们已经知道,在抛硬币的例子中,可以通过一次伯努利试验中出现的k_max来估算n。
那么这种估算方法如何和下面问题有所关联呢?
例如: 统计 APP或网页 的一个页面,每天有多少用户点击进入的次数。同一个用户的反复点击进入记为 1 次,HyperLogLog是这样做的。对于输入的数据,进行下面几个步骤:
1. bit string
通过hash函数,将数据转为比特串,例如输入5,便转为:101。为什么要这样转化呢?
是因为要和抛硬币对应上,比特串中,0 代表了反面,1 代表了正面,如果一个数据最终被转化了 10010000,那么从右往左,从低位往高位看,我们可以认为,首次出现 1 的时候,就是正面。
那么基于上面的估算结论,我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验,同样也就可以根据存入数据中,转化后的出现了 1 的最大的位置 k_max 来估算存入了多少数据。
2. bucket
分桶就是分多少轮。抽象到计算机存储中去,就是存储的是一个以单位是比特(bit),长度为 L 的大数组 S ,将 S 平均分为 m 组,注意这个 m 组,就是对应多少轮,然后每组所占有的比特个数是平均的,设为 P。容易得出下面的关系:
- L = S.length
- L = m * p
- 以 K 为单位,S 占用的内存 = L / 8 / 1024
在 Redis 中,HyperLogLog设置为:m=16834,p=6,L=16834 6。占用内存为=16834 6 / 8 / 1024 = 12K
形象化为:
1 | 第0组 第1组 .... 第16833组 |
3. 对应
现在回到我们的原始APP页面统计用户的问题中去。
- 设 APP 主页的 key 为: main
- 用户 id 为:idn , n->0,1,2,3….
在这个统计问题中,不同的用户 id 标识了一个用户,那么我们可以把用户的 id 作为被hash的输入。即:
hash(id) = 比特串
不同的用户 id,必然拥有不同的比特串。每一个比特串,也必然会至少出现一次 1 的位置。我们类比每一个比特串为一次伯努利试验。
现在要分轮,也就是分桶。所以我们可以设定,每个比特串的前多少位转为10进制后,其值就对应于所在桶的标号。假设比特串的低两位用来计算桶下标志,此时有一个用户的id的比特串是:1001011000011。它的所在桶下标为:11(2) = 1*2^1 + 1*2^0 = 3,处于第3个桶,即第3轮中。
上面例子中,计算出桶号后,剩下的比特串是:10010110000,从低位到高位看,第一次出现 1 的位置是 5 。也就是说,此时第3个桶,第3轮的试验中,k_max = 5。5 对应的二进制是:101,又因为每个桶有 p 个比特位。当 p>=3 时,便可以将 101 存进去。
模仿上面的流程,多个不同的用户 id,就被分散到不同的桶中去了,且每个桶有其 k_max。然后当要统计出 main 页面有多少用户点击量的时候,就是一次估算。最终结合所有桶中的 k_max,代入估算公式,便能得出估算值。
下面是 HyperLogLog 的结合了调和平均数的估算公式,变量释意和LogLog的一样:
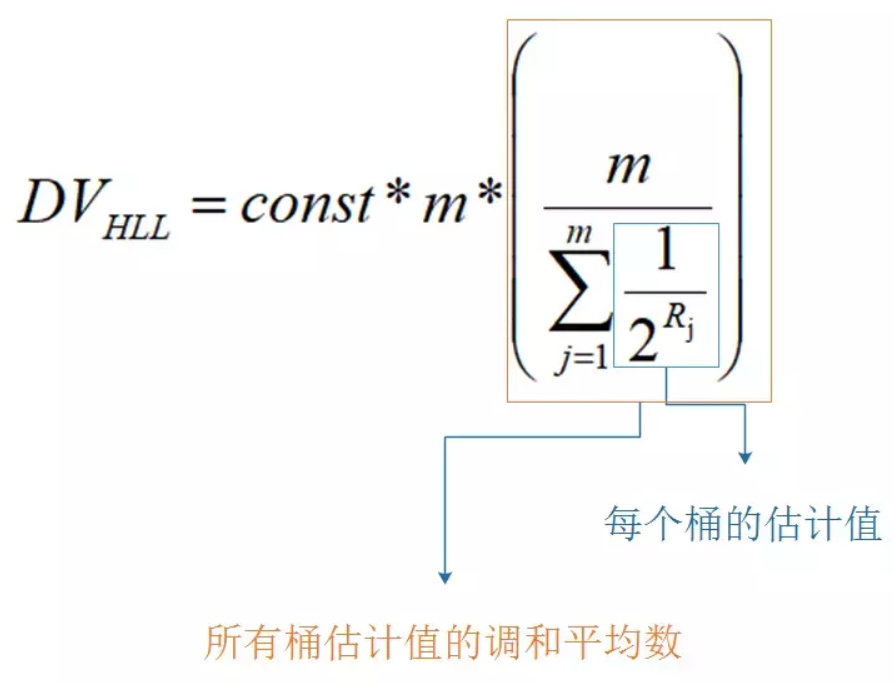
summary
| 伯努利实验 | hyperloglog | |
|---|---|---|
| 一次伯努利实验 | 一直抛硬币,直到出现正面为止 | 每一个bit string 类比为一次伯努利实验,Bit string 从右向左(低位到高位)首次出现1的时候,是正面 |
| n次伯努利实验 | 出现n次正面,抛掷次数为k,n次中最大的k记为k_max,根据2^k_max估算n | n次哈希生成n个bit string代表n次伯努利实验, 根据存入数据转化后出现了1的最大位置k来估算存入了多少数据 |
| m轮n次伯努利实验 | 取m轮的k的调和平均为R,调和平均不容易收到大数值的影响 | 将bit string S 平均分成m组(对应m轮), 长度为p, 字符串长度为L= m*p, 每个string选地位的x位作为bucket index,类比为伯努利实验的轮数 |
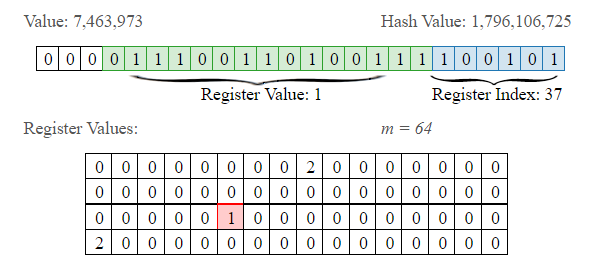
在实现过程中,还需要string中的一小部分当作存储的索引(register index),用于更新register values
参考:
https://www.cnblogs.com/linguanh/p/10460421.html
本文所有图片来源于:
https://www.jianshu.com/p/55defda6dcd2
本文内容参考于:
http://www.rainybowe.com/blog/2017/07/13/神奇的HyperLogLog算法/index.html
手动直观观察 LogLog 和 HyperLogLog 变化的网站: